Herhangi Bir Grupta İki Kişinin Aynı Doğum Gününe Sahip Olma Olasılığı

Soruyu basit bir tespit yaparak çözmeye başlayalım: Eğer ki bir grupta 366 kişi varsa, o grupta iki kişinin aynı doğum gününe sahip olma olasılığı %100 olacaktır. Çünkü 1 yıl içerisinde (29 Şubat göz ardı edilirse) 365 gün vardır ve eğer ki grup içerisinde 366 kişi varsa, mutlaka ve mutlaka bu grupta 2 kişi aynı doğum gününü paylaşmak zorundadır. Peki ya daha küçük gruplarda? Mesela 60 kişilik bir grupta iki kişinin aynı doğum gününe sahip olma olasılığı nedir?

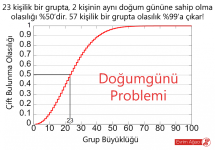
Matematiksel hesaplar göstermektedir ki, 57 kişiden oluşan bir grupta bile 2 kişinin aynı doğum gününe sahip olma olasılığı %99'dur! 23 kişilik bir grupta ise bu %50 dolaylarındadır. Yani 40-50 kişilik bir sınıfta ders verirken bile risk alarak matematiğin gücünü ispatlayabilirsiniz; çünkü sınıfınızda neredeyse kesin olarak yılın aynı gününde doğmuş 2 kişi olacaktır! Adam Fawer'ın Olasılıksız kitabında buna dair bir dramatizasyon bulunmaktadır.

İyi ama neden? Nasıl olur da sadece 57 kişinin bulunduğu bir grupta %99 gibi "neredeyse kesin" bir olasılıkla aynı doğum gününü paylaşan 2 kişi olduğunu söyleyebiliyoruz?

Bunu doğrudan iki kişinin aynı günde doğma olasılığı üzerinden giderek hesaplayabilirsiniz. Ancak daha basiti, "2 kişinin aynı günde doğmama olasılığı"nı hesaplayıp, bu olasılığı %100'den çıkarmak olacaktır. Zira iki insan ya aynı doğum gününü paylaşacaktır, ya da paylaşmayacaktır (iki olasılığın toplamı %100 olmak zorundadır). Olasılıkta bu tip durumlara "ayrışık" ya da "karşılıklı dışlayan" durumlar denir.

Bu durumda matematik açıktır:

Rastgele iki kişi seçin. Bunlardan birinin diğeri ile aynı doğum gününü paylaşmama olasılığı 364/365 (0.9972 ya da %99.72) olacaktır. Çünkü ilk kişi mesela 1 Ocak'ta doğduysa, diğer kişinin 1 Ocak'ta doğmamış olma olasılığı 365 günden 364 gün olacaktır; bu da "364 bölü 365" ile ifade edilir. Diyelim ki ikinci kişi 2 Ocak'ta doğmuş olsun. Bu hesaba dahil edilecek üçüncü bir kişinin 1 Ocak veya 2 Ocak'ta doğmamış olma olasılığı 363/365 (0.9945 ya da %99.45) olacaktır. Dördüncü bir kişinin aynı günü paylaşmama olasılığı 362/365, beşinci bir kişininki 361/365 olacaktır ve bu böyle devam edecektir.

Bunların bir arada (aynı anda) gerçekleşme olasılığını bulmak içinse, bu olasılıkları birbiriyle çarparız. Bunu yapabilme sebebimiz, kişilerden birinin doğum gününün diğerinin doğum gününü etkilemiyor olmasıdır ("ayrışık durumlar"). Örneğin ilk iki kişinin aynı doğum gününü paylaşmama olasılığı (365/365)x(364/365) hesabı ile bulunur ve %99.72'ye eşittir. Yani 2 kişilik bir grupta, kişilerin aynı doğum gününü paylaşmama olasılığı, tam da beklendiği gibi aşırı yüksek bir olasılık olan %99.72'dir. Bir diğer deyişle, rastgele iki kişinin aynı doğum gününe sahip olma olasılığı %100 - %99.72 hesabıyla bulunur ve %0.28'dir. İşte bu nedenle küçük gruplarda aynı doğum gününü paylaşan insan sayısı son derece azdır.

Benzer şekilde, 3 kişiden oluşan bir grupta aynı doğum gününü paylaşmama olasılığı (365/365)x(364/365)x(363/365) = %99.17'dir. Bir diğer deyişle, aynı doğum gününün paylaşılma olasılığı %100-%99.17 = %0.83'tür. Görülebileceği gibi aynı doğum gününe sahip olma olasılığı sadece 1 kişinin eklenmesiyle %0.28'den %0.83'e çıkmıştır! Halen epey küçük; ancak dikkate değer miktarda artıyor.

Bunu eğer 23 kişiye kadar sürdürecek olursanız, şöyle bir hesaplama elde edersiniz:

(365/365)x(364/365)x(363/365)x(362/365)x...x(343/365)

Bu çarpımın sonucunda elde edeceğiniz sayı, yani 23 kişilik bir grupta aynı doğum gününü paylaşan 2 kişinin bulunmuyor olma olasılığı 0.4927'dir, ya da %49.27. Bir diğer deyişle, 23 kişilik bir grupta aynı doğum gününe sahip 2 kişinin bulunma olasılığı %50.73'tür!

Eğer bu işlemi 57 kişiye kadar sürdürecek olursanız, elde edeceğiniz "paylaşmama olasılığı" %1'in altına düşecektir; bir diğer deyişle, aynı doğum gününü paylaşma olasılığı %99'un üzerine çıkacaktır.

İşte tam olarak bu sebeple, eğer ki birilerini etkilemek isterseniz, grup büyüklüğünüzü dikkate alarak (görseldeki grafiği bu amaçla kullanabilirsiniz), kısmen küçük gibi gözüken (örneğin 35 kişilik) bir grupta bile aynı doğum gününü paylaşan iki kişiyi rahatlıkla bulabilirsiniz!